Tak je mi to zase o trochu jasnější .

Takže u Cooley-Tukey algoritmu je jako první krok třeba udělat bitovou inverzi vstupního pole a poté to "motýlkové" zpřeházení viz obrázek?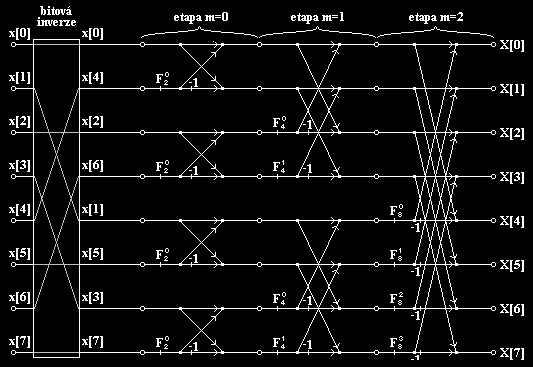

Když budu mít tedy 64 (256) vzorků, tak bude třeba tohle provést 6 resp. 8 zpřeházení (vždy N, kde 2^N = počet vzorků)?
A potom se tam píše, že je třeba provést vlastní FFT. A tam už mi to není jasné, pokoušel jsem si přepsat ten algoritmus do mat. výrazů, ale bez úspěchu. Konkrétně se mi jedná o tenhle kód:

#define N 8

typedef struct{
    double re;
    double im;
}TCplx;

double tsincos[N]={0.000, 1.000, 0.7071, 0.7071, 1.000, 0.000, 0.7071,-0.7071};
TCplx FFTwarr[N];

void FFTditR2(void)
{
    double dsin,dcos;
    double *Fnk;
    TCplx C;
    TCplx *A,*B;
    int s,k;
    int n=1;
    int angf=N;
        
    while(n<N)
    {
        A=&FFTwarr[0];
        B=&FFTwarr[n];     
        Fnk=&tsincos;
        
        for(k=0;k<n;k++)
        {
            dsin=*Fnk++;
            dcos=*Fnk++;
            
            for(s=0;s<angf;s++)
            {
                C.re=A->re*dcos - A->im*dsin;
                C.im=A->re*dsin + A->im*dcos;
                B->re=A->re - C.re;
                B->im=A->im - C.im;
                A->re+=C.re;
                A->im+=C.im;
                A+=2*n;
                B+=2*n;              
            }
            A-=(N-1);
            B-=(N-1);             
            Fnk+=(angf-2);
        }        
        n<<=1;
        angf>>=1;
    }
}